Zaproponowany w tym rozdziale sposób nauki improwizacji nazwijmy w uproszczeniu „metodą permutacji”.
Przypomnijmy dźwięki skali majorowej – C-dur:
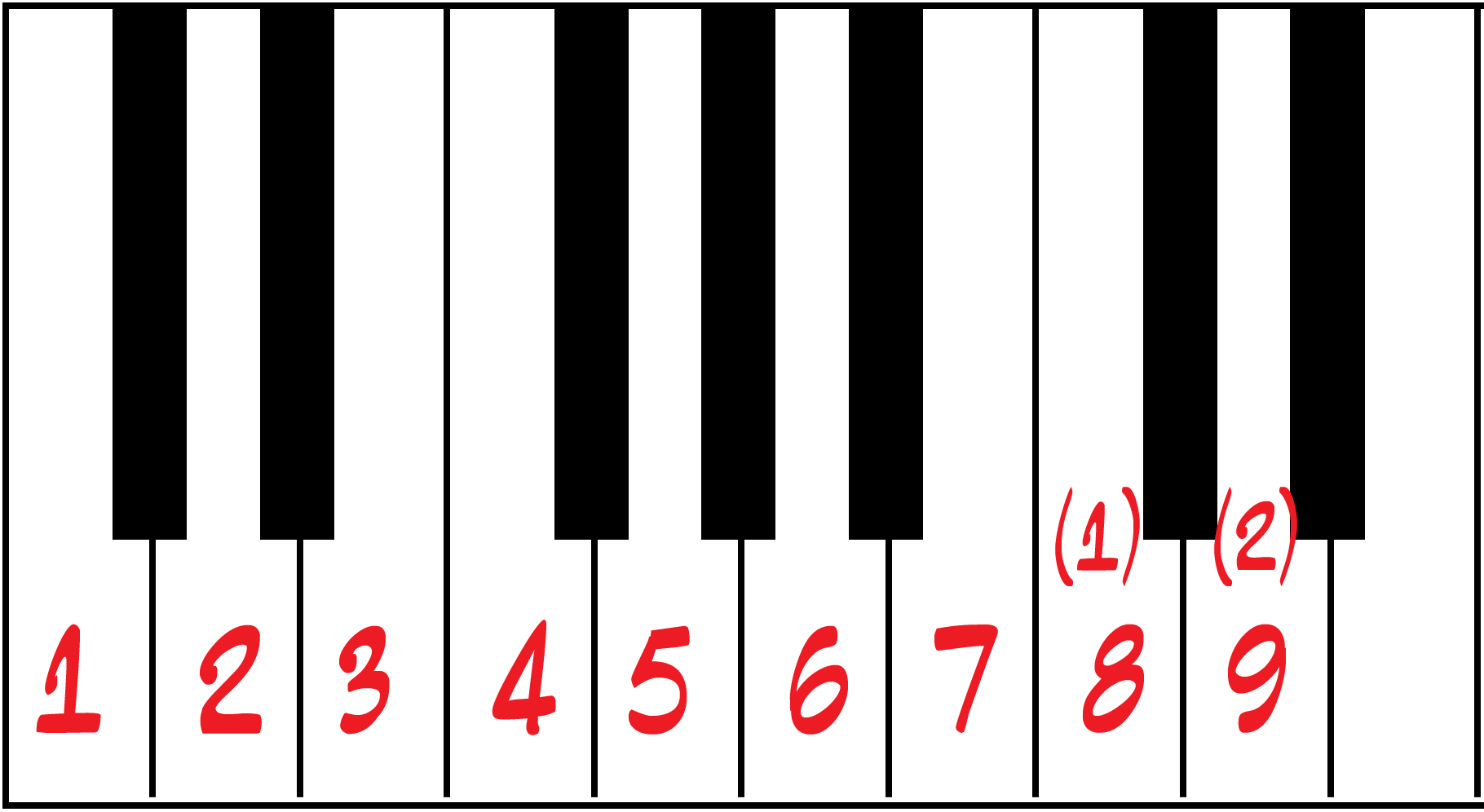 |
Najczęściej spotykaną sytuacją w improwizacji jest improwizacja ósemkami, a funkcje zmieniają się co pół taktu. Masz zatem do wyboru cztery nuty. Dla Cmaj7 mogą być to:
Możesz rozpocząć od prymy (1), tercji (3) sekundy (2) lub kwinty (5), masz zatem pewną liczbę (24) możliwości:
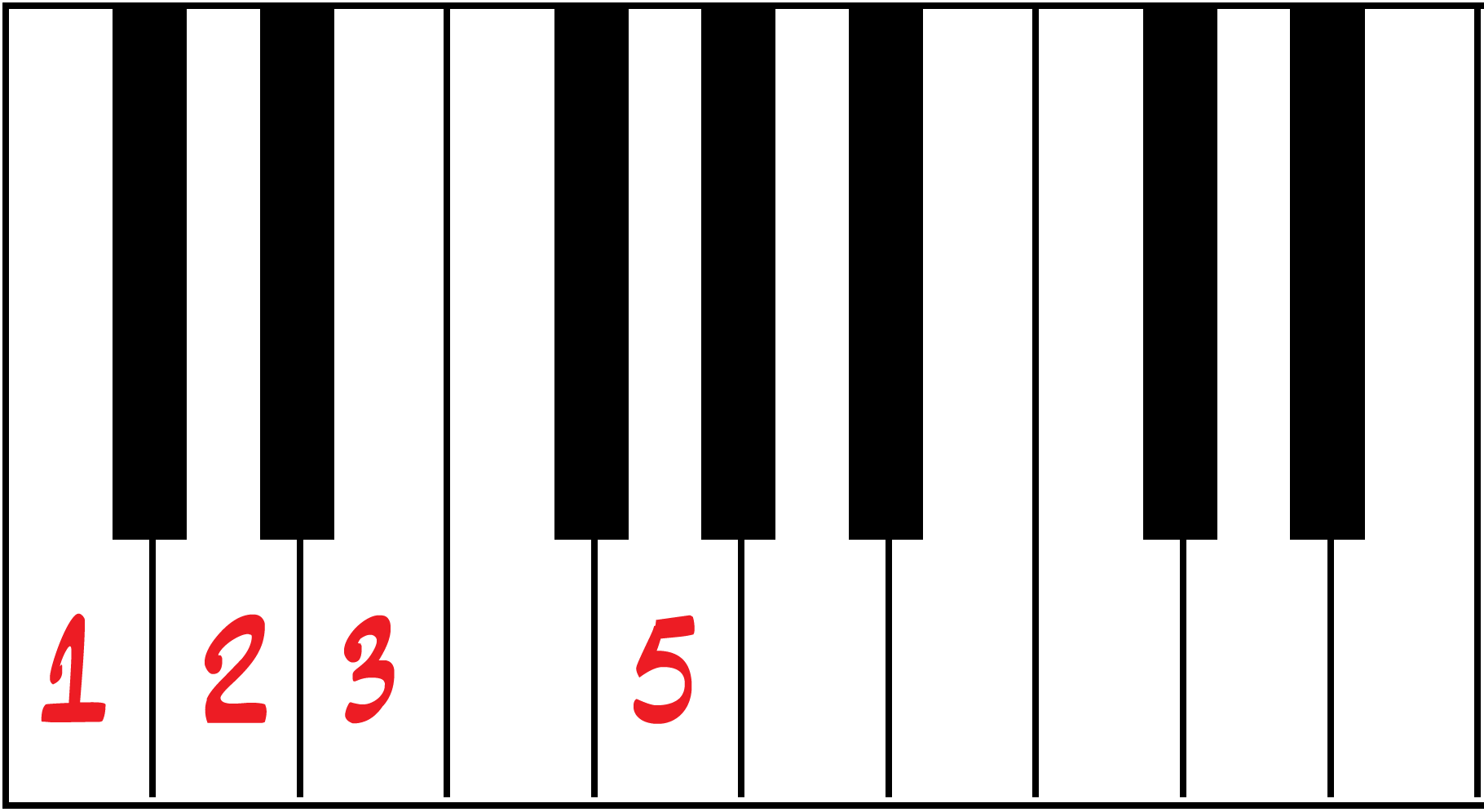 |
| 1325 | 1352 | 1235 | 1253 | 1532 | 1523 |
| 3152 | 3125 | 3215 | 3251 | 3512 | 3521 |
| 2135 | 2153 | 2315 | 2351 | 2513 | 2531 |
| 5132 | 5123 | 5312 | 5321 | 5213 | 5231 |
Takie wykorzystanie elementów zbioru (nut) nazywamy permutacją. Myślenie i ćwiczenie permutacjami nut może być przydatne zwłaszcza w utworach o bogatej harmonii.
Znakomicie nadaje się do oswajania z akordami. Powoduje przyzwyczajenie do grania prawidłowych dźwięków na właściwe akordy. Jednocześnie, nie musisz przywoływać z pamięci wszystkich dźwięków skali, wystarczy cztery z nich. W procesie podejmowania natychmiastowych decyzji nakładania dźwięków na akord pozwoli to na bezbłędne granie, mimo często zmieniających się akordów lub szybkich temp.
Trochę matematyki (nie musisz czytać, chociaż warto wiedzieć:)).
Permutacją jest ustawienie wszystkich elementów zbioru w dowolnej kolejności. Definicja: permutacją zbioru n-elementowego nazywamy każdy n-wyrazowy ciąg utworzony ze wszystkich elementów tego zbioru. Jego liczba wyraża się wzorem n! (n silnia).
Pn=n!
Ta definicja dotyczy zbiorów bez powtórzeń.
P4=4!=24, ponieważ 1*2*3*4=24
P5=5!=120
P6=6!=720
P7=7!=5040
P8=8!=40320
Zatem używając skali siedmiodźwiękowej masz ponad pięć tysięcy możliwości, a przy skali ośmiodźwiękowej – ponad czterdzieści tysięcy.
Użycie wszystkich dwunastu dźwięków daje:
P12=12!=479001600
możliwości.
Możliwości kombinacji dźwięków znacznie rosną, jeśli rozważyć powtórzenia elementów.
Permutacją z powtórzeniami zbioru n-elementowego, nazywamy każdy ciąg n-wyrazowy utworzony z elementów tego zbioru, wśród których pewne elementy powtarzają się odpowiednio n1,n2,…,nk razy.
Liczba permutacji z powtórzeniami zbioru n-elementowego, wśród których pewne elementy powtarzają się odpowiednio n1,n2,…,nk razy wyraża się wzorem:
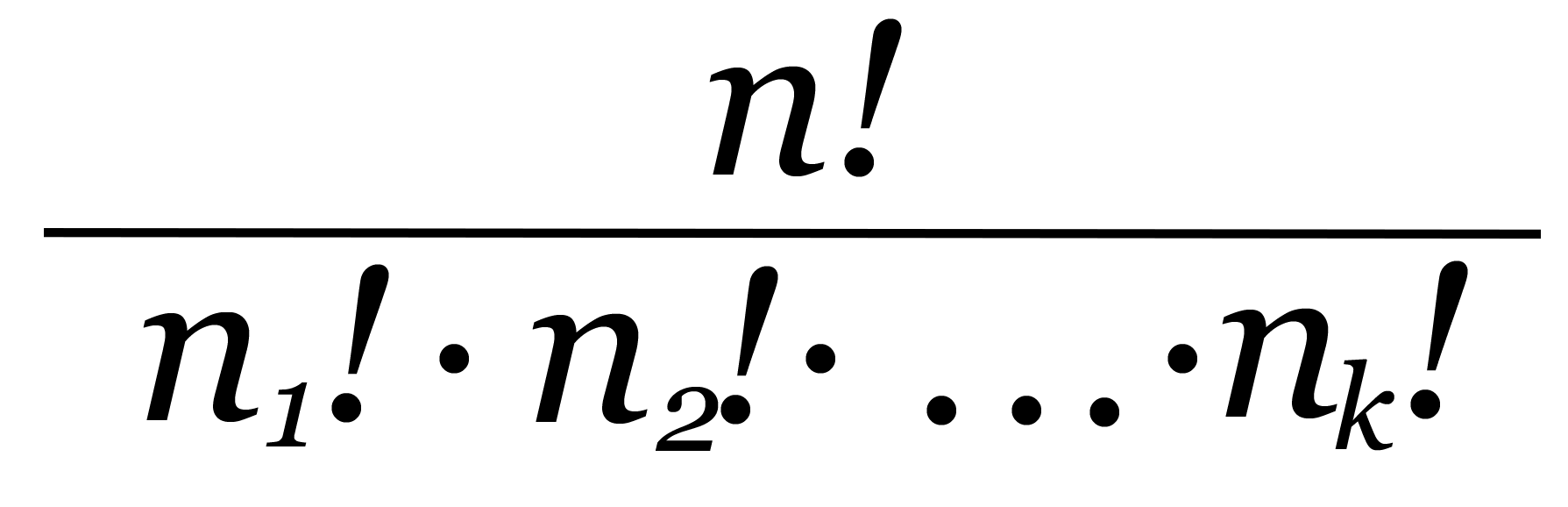 |
Zatem z melodyjki: c-d-e-d-c można ułożyć:
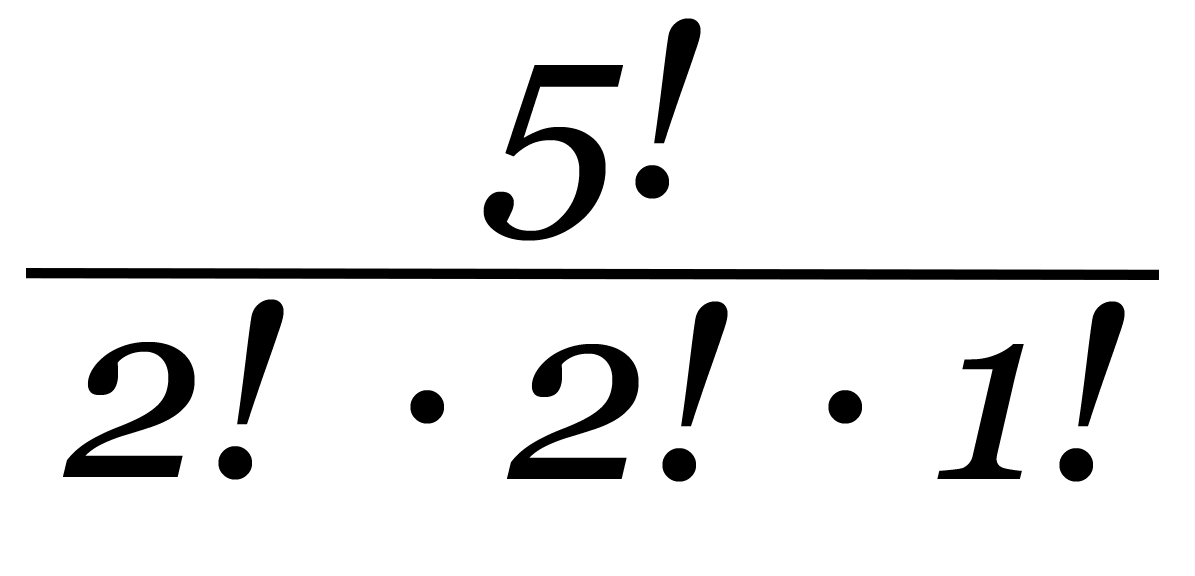 |
120:4=30
trzydzieści różnych melodii!
Permutacje dźwięków skali majorowej jońskiej dla akordu Cmaj7 w tonacji C-dur.
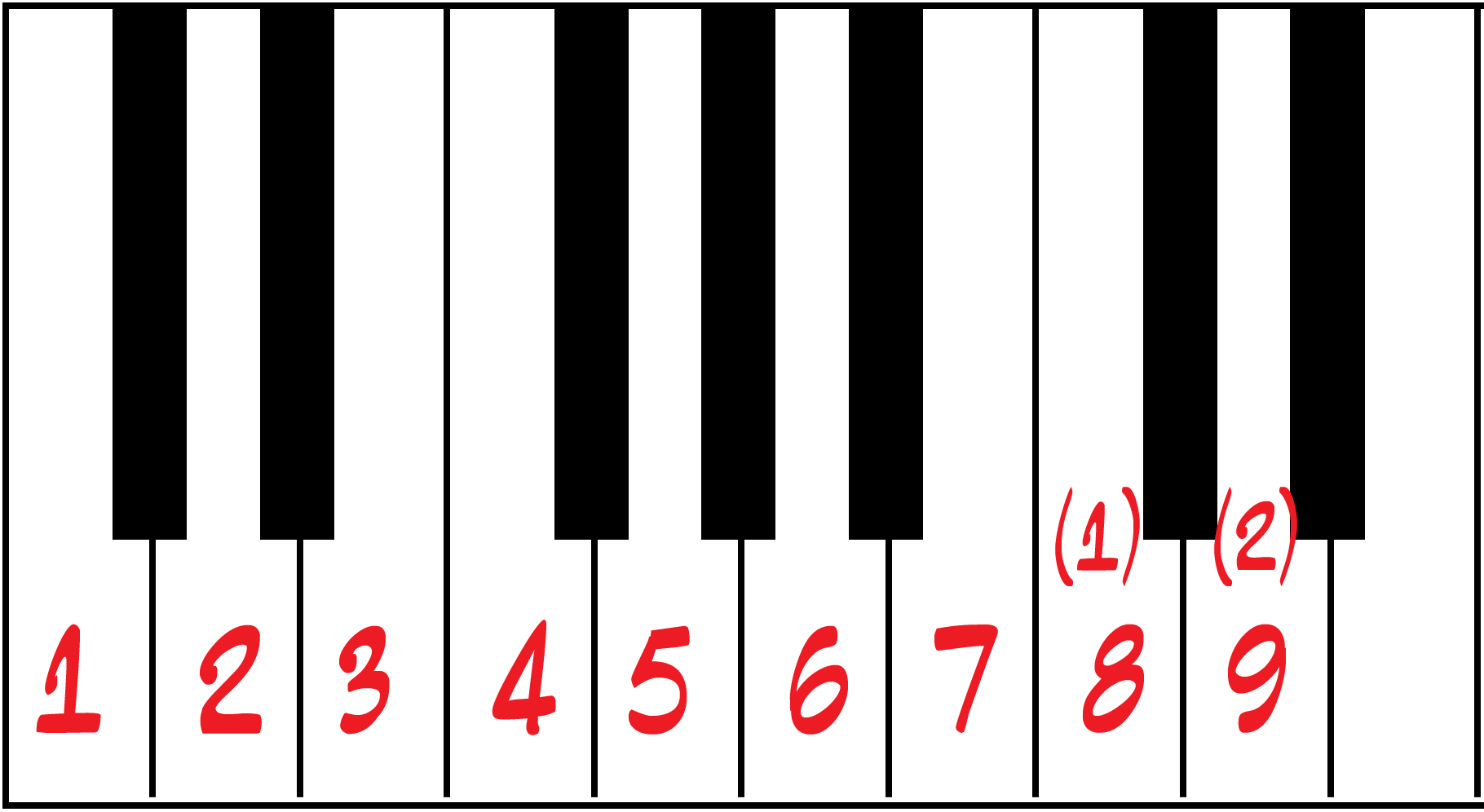 |
    |
| 1. | 1325 | 1352 | 1235 | 1253 | 1532 | 1523 |
| 2. | 3152 | 3125 | 3215 | 3251 | 3512 | 3521 |
| 3. | 2135 | 2153 | 2315 | 2351 | 2513 | 2531 |
| 4. | 5132 | 5123 | 5312 | 5321 | 5213 | 5231 |
Przykład innej tonacji – Ab maj (akord Abmaj).
 |
Przykład innej tonacji – A maj (akord Amaj).
 |
Przykład innej tonacji – F maj (akord Fmaj).
 |
Przykład innej tonacji – D maj (akord Dmaj).
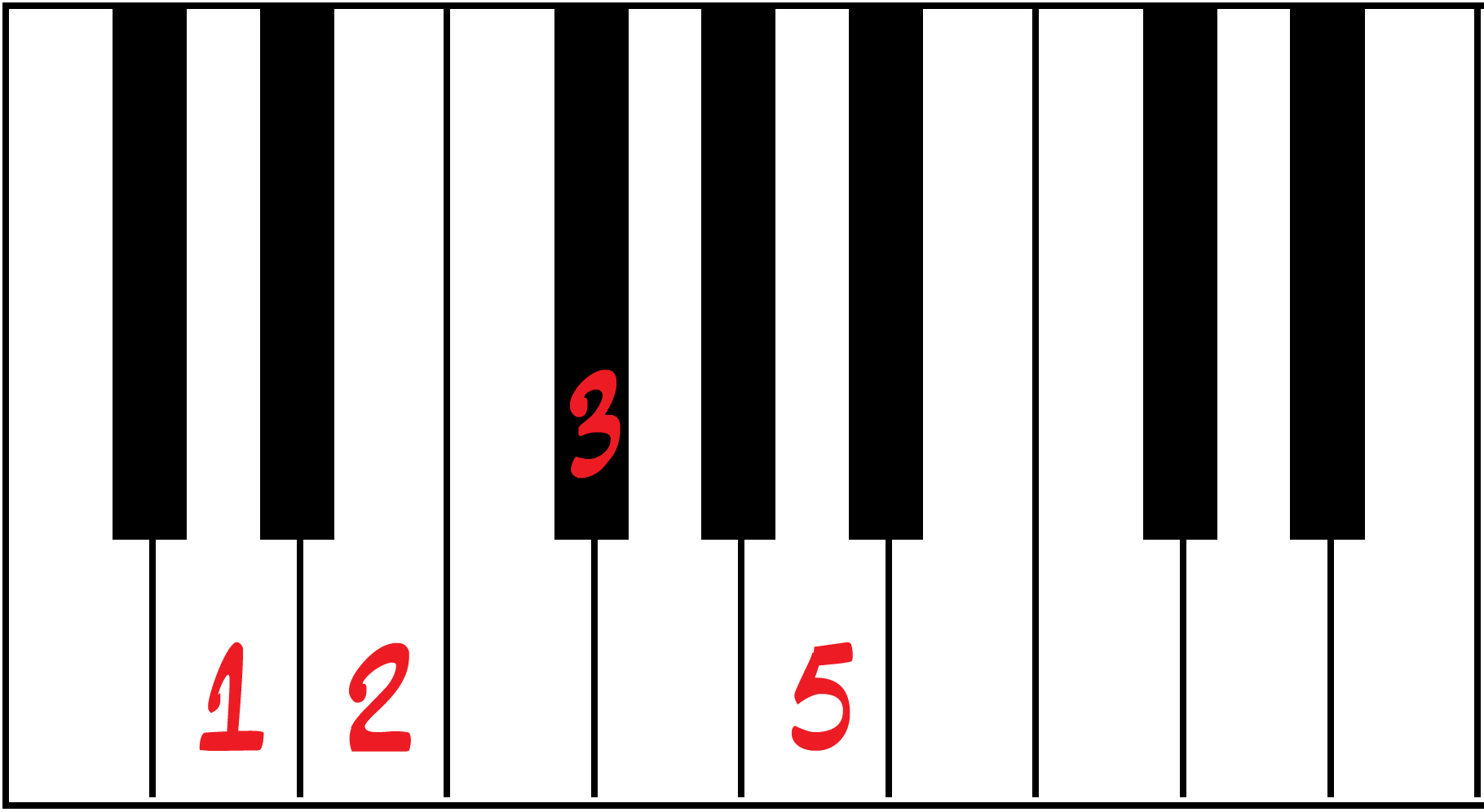 |